中国古代,在数学方面最大的成就,是在某种程度上普及了“九九乘法表”。一一得一,二二得四,张口就来。在此基础上,脑子好用点的,百位以内加减乘除,比用计算器算得还快。而且,还传流下来一件神器——算盘!啪啪啪一打,看得洋人目瞪口呆!

这也给了当代中国人diss外国人数学不好的勇气:
“美国小学生,五年级了,8+8还得掰指头!”
“不给个计算器,美国佬8X8都不知道等于几!”
“美国考研究生的数学题还没有我初中的数学题难!”
这样的话听多了,让人倍感恍惚。陈省身干吗要去美国留学,难道是去普渡众生?丘成桐是怎么拿到菲尔兹奖的,难道是充美国话费送的?
暂且放下美国佬“学霸从严教、学渣放了羊”的精英教育模式不表。先来回想一下,我们的数学是怎么”好“起来的?答案是:背呗!
大概从小学二年级开始,老师要求背诵“九九乘法表”。老师对我们很客气:“要求也不高求积分的公式,正着背、倒着背、横着背、竖着背、斜着背,都得背过”,“什么?背不过?!背不过,你好意思自称'炎黄子孙'吗?”
于是,每天都要像背古文一样,背诵“九九乘法表”。而且,每到暑假,西游记重播,还能帮你复习N遍”九九八十一“。
耳熟能详的程度仅次于国歌!
我们对世界万物的认知方法,其一是原理,其二是经验。第一个遇到8X8=?这样问题的人,一定用8个8累加计算过,可能还反复验证过。于是,才得出结论:8X8=64。到此,原理就可以总结成经验,传播给下一个以及更多的人。而当经验广泛传播后,你再遇到一个用8个8累加计算8X8=?的人,脸上立马泛出鄙夷的神态:“这货莫不是个傻瓜?”
难道,用8个8累加计算得出8X8=64的计算原理错了吗?
当然没错,简直不要太正确好吧!只是它太简单了,你瞧不上:这还用算吗?!
老子在《道德经》里讲:道生一,一生二,二生三求积分的公式,三生万物。对于世界构成来讲,不管复杂与简单,它的底层逻辑是一以贯之的。用原理解决问题,可以贯穿始终;用经验解决问题,只能停留在一个特定的区间里。
掌握经验数学没有错,但不能让经验成为判断客观存在的唯一依据。
比如,我们要求一个三角形的面积,如下图:
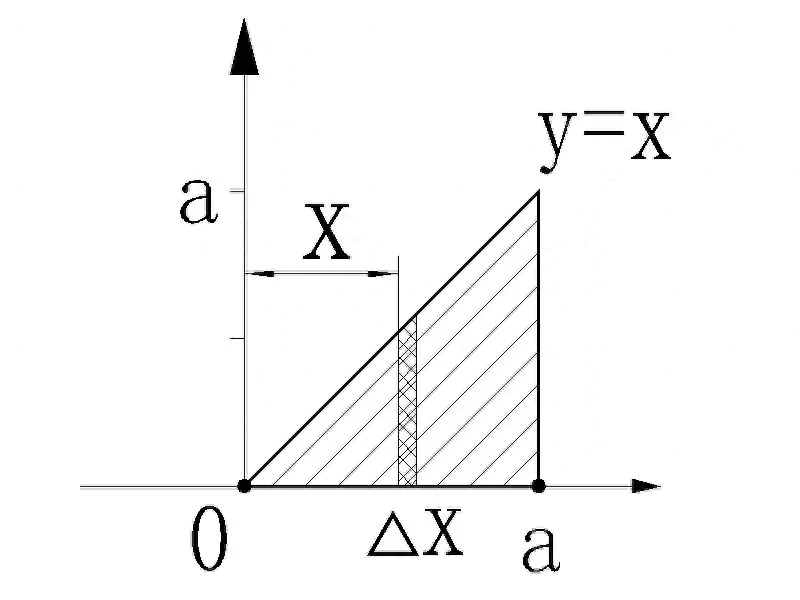
一目了然,三角形的面积S=1/2 a^2。这个结果,是由一个边长为a的正方形的面积公式S=a^2推导来的,是经验公式。
我们再来用微积分的方法来推导一下:S=∫xdx,x∈[0,a]=1/2 a^2。结果是一样的。可见,没有经验公式,我们也可以从原理上去推导出来。
如果,我们往复杂的方向推进,经验数学还有效吗?
比如我们求一个圆的面积,如下图:

这时候,已经不完全是靠经验去求圆的面积公式了。我们需要借助极限近似的思想去解析它,把圆分割成小扇形,再拼合成一个矩形,得:S=π r^2。
我们再来用微积分的方法来推导一下。选取第一象限做计算单元,再找到可积的微分单元√(r^2-x^2)dx,x∈[0,r]
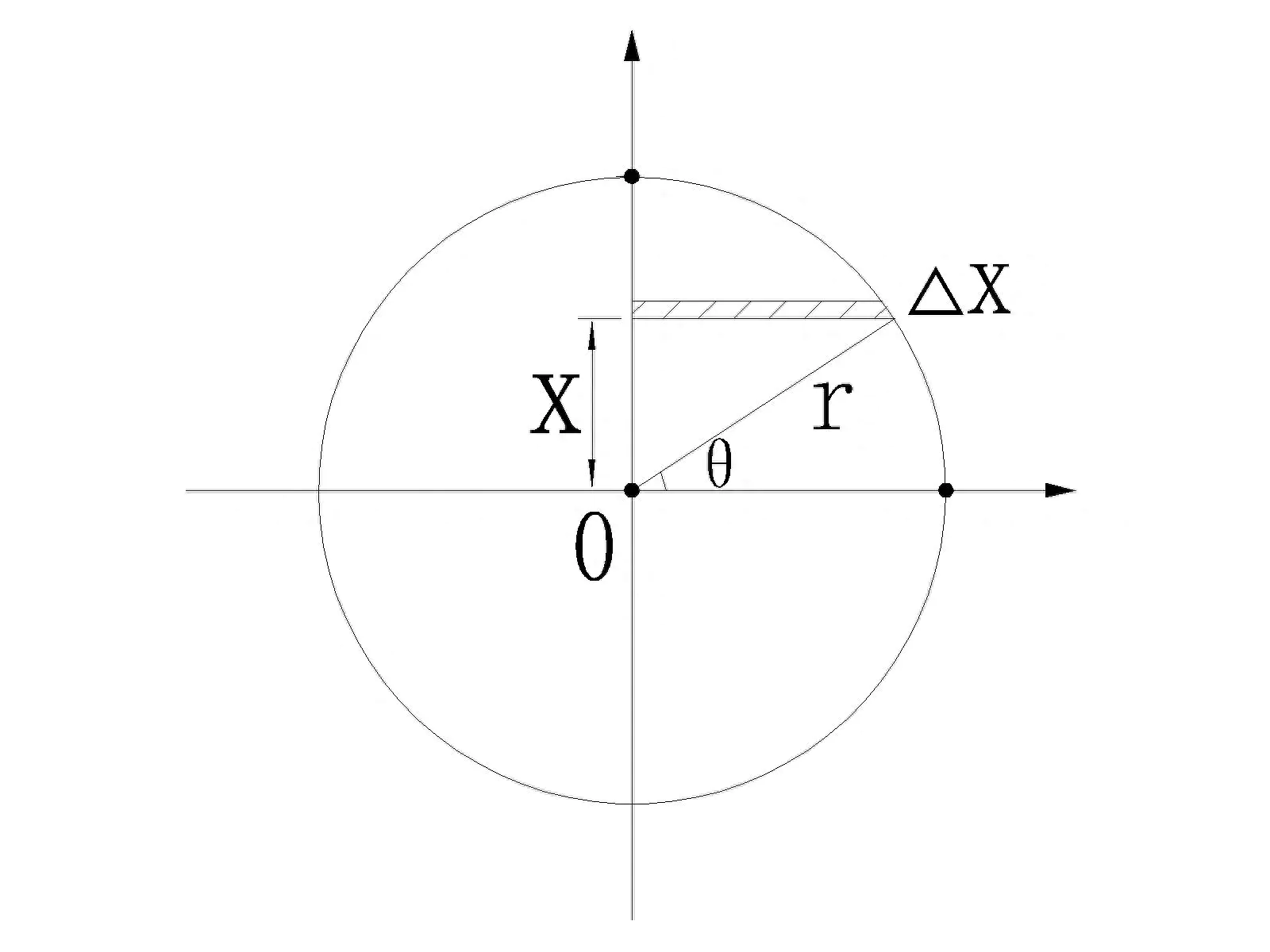
对其积分,得S/4=∫√(r^2-x^2)dx,x∈[0,r]
令x=rcosθ,则√(r^2-x^2)=rsinθ
dx=-rsinθdθ,得S/4=∫rsinθ*(-rsinθ)dθ,θ∈[0,π/2]=1/4 π r^2(略去中间过程)
则S=π r^2。
如果不用θ替代x,我们也可以求出√(r^2-x^2)dx的不定积分通式:
∫√(r^2-x^2)dx=x/2*√(r^2-x^2)+1/2 r^2*arc sin(x/r)+C
用这个通式,求定积分,结果也是S=π r^2。
再复杂一些的图形,用经验公式已经没法解了。但用微积分的原理,多难的都能找到解法。
和8个8累加的原理计算沉淀为8X8=64的经验公式一样,微积分的原理计算也积累下许多经验公式。上面那道公式∫√(r^2-x^2)dx=x/2*√(r^2-x^2)+1/2 r^2*arc sin(x/r)+C,就是从积公表里查到的。如下图,第67。

整个积分表几乎涵盖了乘积、开方、幂次方、指数、对数、三角函数、双曲函数等各类函数的表达形式。只要我们写得出导函数,就可以在积分表中找到对应的积分,让整体计算变得简单容易。
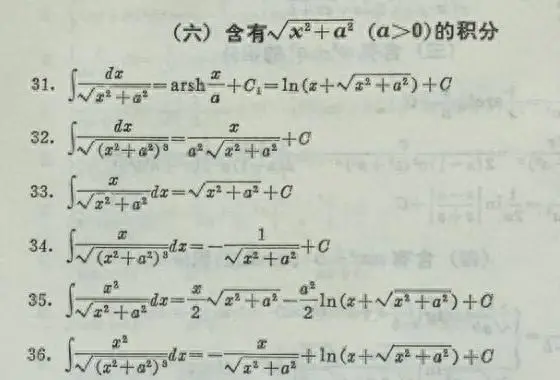

除了这个复杂的积分表,我们还有简单一些的常用积分表:
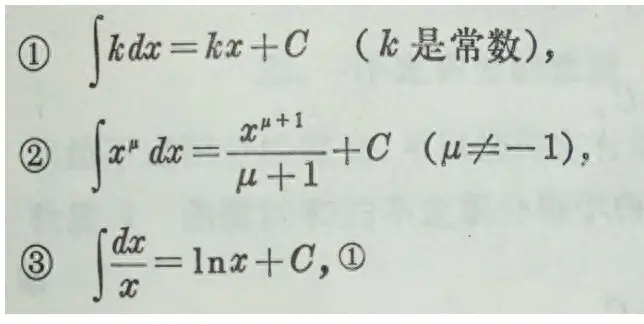

学习微积分,这些不定积分的式子是要熟记的,相当于微积分领域的“九九乘法表”。
读到此处,不知道还有多少人能留存住diss外国人数学不好的勇气。
有人讲,这些什么积分表,普通外国人都会吗,他们记得住吗?我觉得大部分美国佬肯定不会,这比8X8=?可难多了,但这不影响美国是个数学强国。代表一国的数学水平,那是数学家的事。就像打仗是军人的事,评价一个农夫花拳绣腿的水平有多高,是没有意义的!
论起数学来,逻辑很重要!
娜娜项目网每日更新创业和副业教程
网址:nanaxm.cn 点击前往娜娜项目网
站 长 微 信: nanadh666

