
编辑搜图
请点击输入图片描述
在历年公务员考试之中,行测图形推理一直占有稳定的比例,其中,空间折叠题目在每年的考试中出现频率较稳定,也是同学们反映比较难解的题目,尤其在考试时间本就不够用的情况下,又往往耗时颇久。那么我们如何缩短做题时间,更快选出答案呢?对于图形推理中较难的空间折叠题目来说,合理利用立方体自身特点,可以帮助我们更快的排除错误选项,确定答案。下面,通过一道例题,教你如何快速解决空间折叠题目。
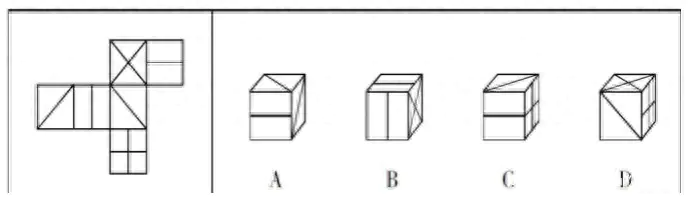
编辑搜图
请点击输入图片描述
对于这样一道空间折叠的题目,很多同学认为没有好的空间想象能力,这类题目耗时太久,准确率不高,干脆放弃。其实不然,在空间折叠的题目中,“相对面排除法”可以帮助我们解决大部分问题。以上面的题目为例:
娜娜项目网每日更新创业和副业项目
网址:nanaxm.cn 点击前往娜娜项目网
站 长 微 信: nanadh666
首先,我们需要明确,在一个正立面体的六个面中,一共有三组相对面,且每组相对面中的两个面互不相邻。那么,我们只需要在左侧的平面展开图中,找到三组相对面,再到右侧的选项中对照,是否有相对面相邻的情况即可,若出现相对面相邻的选项,我们便可直接排除。
接着,我们如果在平面展开图中确定三组相对面呢?我们只要记住:在平面展开图中相隔连续一整行或一整列的两个面互为相对面即可。通过这个要点,我们便可在题中的展开图中确定,三组相对面为:1-5,2-4,3-6。
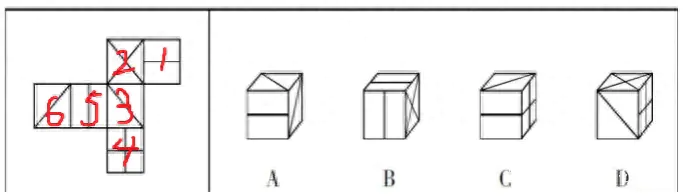
编辑搜图
请点击输入图片描述
最后折叠空间折叠空间,我们明确了相对面后,对照右侧选项。我们发现A项中,上面和右面为展开图中3、6两个面,而这两面互为相对面,不能相邻,排除。B项中,上面和正面为展开图中1、2两个面,而这两个面同样互为相对面,不能相邻,排除。C项,三个面并不存在相对面,保留。D项中,上面和右面分别为展开图中的2、4两个面,这两面同样互为相对面,不能相邻,排除。综上,我们不难判断,本题的答案为C选项。
通过上面的题目大家会发现,了解立方体自身特性并充分加以利用,即使空间想象能力并不强的同学们,也可以通过“相对面排除法”快速排除错误选项,甚至确定答案。因此,大家在面对空间折叠题目时,应克服固有恐惧心理,不要轻易放弃,认真学习并掌握方法,就可以快速锁定答案,难题也会变成加分题。
娜娜项目网每日更新创业和副业项目
网址:nanaxm.cn 点击前往娜娜项目网
站 长 微 信: nanadh666

