有理数的意义
【学习目标】
1.掌握用正负数表示实际问题中具有相反意义的量;
2.理解正数、负数、有理数的概念;
3. 掌握有理数的分类方法,初步建立分类讨论的思想.
【要点梳理】
要点一、正数与负数
像+3、+1.5、、+584等大于0的数,叫做正数;像-3、-1.5、、-584等在正数前面加“-”号的数,叫做负数.
要点诠释:
(1)一个数前面的“+”“-”是这个数的性质符号, “+”常省略,但 “-”不能省略.
(2)用正数和负数表示具有相反意义的量时,哪种为正可任意选择,但习惯把“前进、上升”等规定为正,而把“后退、下降”等规定为负.
(3)0既不是正数也不是负数,它是正数和负数的分界线.
要点二、有理数的分类
(1)按整数、分数的关系分类: (2)按正数、负数与0的关系分类:

要点诠释:
(1)有理数都可以写成分数的形式,整数也可以看作是分母为1的数.
(2)分数与有限小数、无限循环小数可以互化,所以有限小数和无限循环小数可看作分数,但无限不循环小数不是分数,例如.
(3)正数和零统称为非负数;负数和零统称为非正数;正整数、0、负整数统称整数.
【典型例题】
类型一、正数与负数
1.(2016•广州)中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果收入100元记作+100元.那么﹣80元表示()
A.支出20元 B.收入20元 C.支出80元 D.收入80元
【思路点拨】在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
【答案】C
【解析】解:根据题意,收入100元记作+100元,
则﹣80表示支出80元.
故选:C.
【总结升华】本题考查了正数和负数,解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量.
举一反三:
【高清课堂:有理数的意义 356786概念的应用例3(1)】
【变式1】(2015•太仓市模拟)一种大米的质量标识为“(50±0.5)千克”,则下列各袋大米中质量不合格的是()
A.50.0千克 B.50.3千克 C.49.7千克 D.49.1千克
【答案】D.
解:“50±0.5千克”表示最多为50.5千克,最少为49.5千克.
【变式2】(1)如果收入300元记作+300元,那么支出500元用___________ 表示,0元表示__________ .
(2)若购进50本书,用-50本表示,则盈利30元如何表示?
【答案】(1)-500元;既没有收入也没有支出. (2)不是一对具有相反意义的量,不能表示.【变式3】如果60m表示“向北走60m”,那么“向南走40m”可以表示为( ).A.-20m B.-40m C.20m D.40m【答案】B
2.体育课上,华英学校对九年级男生进行了引体向上测试,以能做7个为标准,超过的次数记为正数,不足的次数记为负数,其中8名男生的成绩如下:2,-1,0,3,-2,-3,1,0
(1)这8名男生有百分之几达到标准?
(2)他们共做了多少引体向上?
【答案与解析】(1)由题意可知:正数或0表示达标,
而正数或0的个数共有5个,所以百分率为:;
答:这8名男生有62.5%达到标准.
(2)(7+2)+(7-1)+7+(7+3)+(7-2)+(7-3)+(7+1)+7=56(个)
答:他们共做了引体向上56个.
【总结升华】一定要先弄清“基准”是什么.
类型二、有理数的分类
【高清课堂:有理数的意义 356786 概念的应用例2】
3.下面说法中正确的是( ).
A. 非负数一定是正数.
B. 有最小的正整数,有最小的正有理数.
C.一定是负数.
D .正整数和正分数统称正有理数.
【答案】D
【解析】(A)不对,因为非负数还包括0;(B) 最小的正整数为1,但没有最小的正有理数;(C)不对,当为负数或0时,则为正数或0,而不是负数;(D)对
【总结升华】一个有理数既有性质符号,又有除性质符号外的数值部分,两者合在一起才表示这个有理数.
举一反三:
【变式1】判断题:
(1)0是自然数,也是偶数.( ) (2)0既可以看作是正数,也可以看成是负数.( )
(3)整数又叫自然数.( ) (4)非负数就是正数,非正数就是负数.( )
【答案】√, ,,
【变式2】下列四种说法,正确的是( ).(A)所有的正数都是整数 (B)不是正数的数一定是负数(C)正有理数包括整数和分数 (D)0不是最小的有理数
【答案】D
4.请把下列各数填入它所属于的集合的大括号里.1, 0.0708, -700, -3.88, 0, 3.14159265, , .正整数集合:{ …}, 负整数集合:{ …},整数集合:{ …}, 正分数集合:{ …},
负分数集合:{ …},分数集合:{ …},
非负数集合:{ …},非正数集合:{ …}.
【答案】正整数: 1;负整数:-700;整数:1,0,-700;正分数:0.0708,3.14159265,;负分数: -3.88,;
分数:0.0708,3.14159265,,-3.88,;
非负数: 1,0.0708, 3.14159265,0,;
非正数:-700, -3.88, 0,

【总结升华】填数的方法有两种:一种是逐个考察,一一进行填写;二是逐个填写相关的集合,从给出的数中找出属于这个集合的数.此外注意几个概念:非负数包括0和正数;非正数包括0和负数.
举一反三:
【变式】(2014秋•惠安县期末)在有理数、﹣5、3.14中,属于分数的个数共有个.
【答案】2.
类型三、探索规律
5.某校生物教师李老师在生物实验室做实验时,将水稻种子分组进行发芽试验:第1组取3粒,第2组取5粒,第3组取7粒,第4组取9粒,.按此规律,那么请你推测第n组应该有种子是粒.
【答案】()
【解析】第1组取3粒,第2组取5粒,第3组取7粒,第4组取9粒,,由此我们观察到的粒数与组数之间有一定关系:,,,,,按此规律,第n组应该有种子数()粒.
【总结升华】研究一列数的排列规律时最大的负整数是多少,其中的数与符号往往都与序数有关.
举一反三:
【变式1】有一组数列:2,-3,2,-3,2,-3,,根据这个规律,那么第2010个数是:
【答案】-3
【变式2】观察下列有规律的数:根据其规律可知第9个数是:
【答案】1/90
【巩固练习】
一、选择题
1. (2014•甘肃模拟)下列语句正确的()个
(1)带“﹣”号的数是负数;
(2)如果a为正数,则﹣a一定是负数;
(3)不存在既不是正数又不是负数的数;
(4)0℃表示没有温度.
A. 0 B. 1 C. 2 D. 3
2.关于数“0”,以下各种说法中,错误的是 ( ) A.0是整数 B.0是偶数 C.0是正整数 D.0既不是正数也不是负数 3.如果规定前进、收入、盈利、公元后为正,那么下列各语句中错误的是 ( ) A.前进-18米的意义是后退18米 B.收入-4万元的意义是减少4万元 C.盈利的相反意义是亏损 D.公元-300年的意义是公元后300年 4.一辆汽车从甲站出发向东行驶50千米,然后再向西行驶20千米,此时汽车的位置是 ( ) A.甲站的东边70千米处 B.甲站的西边20千米处 C.甲站的东边30千米处 D.甲站的西边30千米处
5.在有理数中,下面说法正确的是( )
A.身高增长和体重减轻是一对具有相反意义的量
B.有最大的数
C.没有最小的数,也没有最大的数
D.以上答案都不对


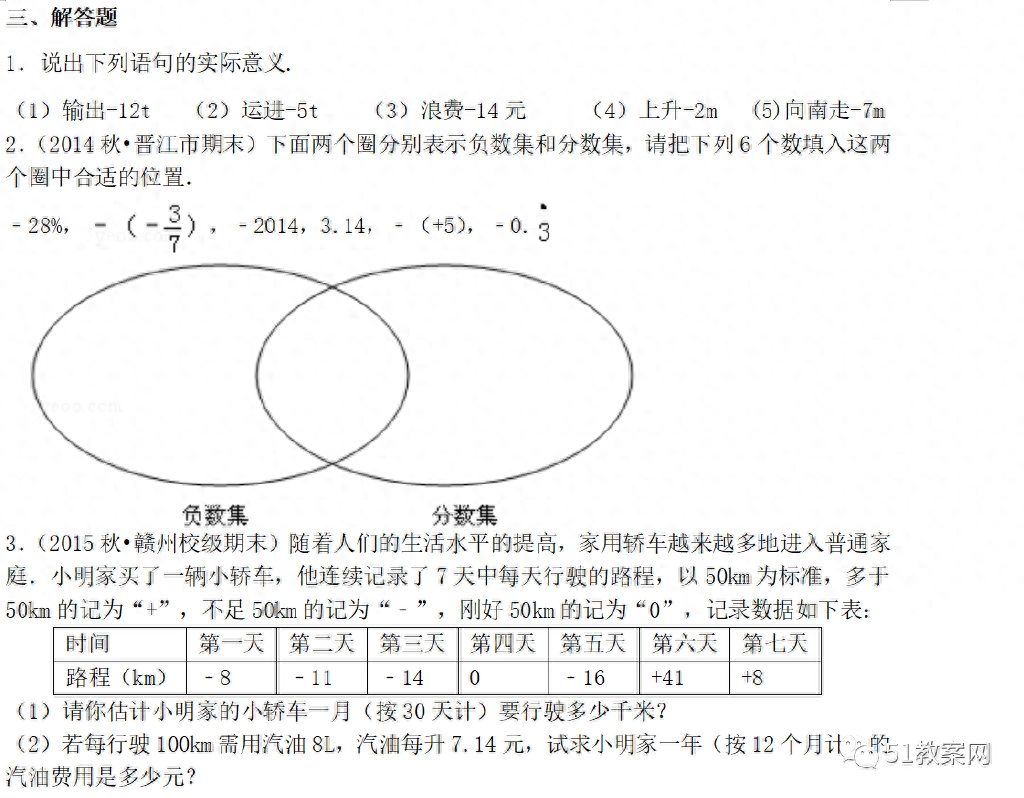

【答案与解析】
一、选择题
1.【答案】B
【解析】(1)带“﹣”号的数不一定是负数,如﹣(﹣2),错误;
(2)如果a为正数,则﹣a一定是负数,正确;
(3)0既不是正数也不是负数,故不存在既不是正数又不是负数的数此表述错误;
(4)0℃表示没有温度,错误.
综上,正确的有(2),共一个.
2.【答案】C
【解析】0既不是正数也不是负数,但0是整数,是偶数,是自然数.
3. 【答案】D
【解析】D错误,公元-300年的意义应该是公元前300年.
4. 【答案】 C
【解析】画个图形有利于问题分析,向东50千米然后再向西20千米后显然此时汽车在甲站的东边30千米处.
5.【答案】C
【解析】A错误最大的负整数是多少,因为身高与体重不是具有相反意义的量;B错误,没有最大的数也没有最小数;C对.
6. 【答案】B


娜娜项目网每日更新创业和副业教程
网址:nanaxm.cn 点击前往娜娜项目网
站 长 微 信: nanadh666

