前面给大家讲过了 ->
这一节小甲鱼给大家谈谈组合数(Combinations)。

组合数的概念
组合数(Combinations)是组合数学中的其中一个概念,
它表示从 n 个不同元素中取出 m 个元素(m ≤ n)的所有可能性。
不过跟排列数不一样,组合数对元素的排列顺序并没有要求!
(也就是说 AB 和 BA 在组合数中是算作相同的)
举个简单的例子,假设我们有三个不同颜色的小球:

当我们从中拿出 1 颗小球时,那么可能是拿到 A,也可能是拿到 B,当然 C 也是有可能被拿到的,所以有 3 种不同的组合(此时组合数为 3)
当我们从中拿出 2 颗小球时,那么所有存在的可能性是:AB、AC、BC,一共有 3 种不同的组合(此时组合数为 3)
当我们从中拿出 3 颗小球时,那么所有存在的可能性是:ABC,由于组合数不考虑排序,所以只有这 1 种组合(此时组合数为 1)
和排列数一样排列组合公式,组合数也有一个计算公式:
表示从 n 个不同元素中取出 m 个元素(m ≤ n)的所有可能性(元素的顺序不重要)。
组合数公式的推导过程
下面是排列数公式:
大家对比一下,跟组合数公式有啥子不一样的?
组合数其实就是在排列数的基础上排列组合公式,再去除以 m! 的即可~
那为什么是除以 m!,而不是 n! 或者别的什么东西呢?
来,我们思考一下,还是上面的 A、B、C 三颗小球,从中任意选 2 个出来
构成的所有排列数是:AB、AC、BC、BA、CA、CB
构成的所有组合数是:AB、AC、BC
大家一对比就很容易发现,所谓组合数,其实就是在排列数的基础上去掉重复的组合。
那好,重复的组合如何算?
比如选择 2 个元素,有多少种重复的组合?
其实就是 2! 种(AB、BA)。
娜娜项目网每日更新创业和副业项目
网址:nanaxm.cn 点击前往娜娜项目网
站 长 微 信: nanadh666
如果选择 3 个元素,那么重复的组合就是 3! 种。
为什么呀?
因为所谓的 “m 个元素重复的组合数量”,其实就是求排列数 P(m, m) 嘛。
对不对?
比如 3 个元素,还是 A、B、C,那么它的排列数就是:
P(3, 3),ABC、ACB、BAC、BCA、CAB、CBA,一共 6 种
(它们都是相同的元素,但有 6 种不同排列方式)
因此,想要求出 C(n, m),其实就是先求出 P(n, m),再除去重复的 P(m, m) 即可~
我们可以推导出组合数的公式就是这么来的:
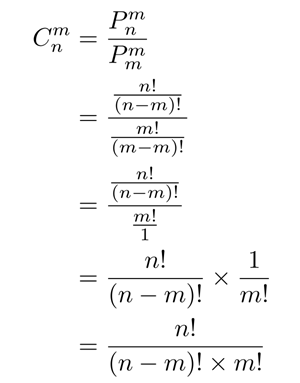

戳原文,更有料!
娜娜项目网每日更新创业和副业项目
网址:nanaxm.cn 点击前往娜娜项目网
站 长 微 信: nanadh666

